1 Introduction
왜 multi-head 가 single attention에 비해 좋은 성능을 내는지 그 원인이 정확하게 이해되지 않는다. (아마 perspective 의 다양성이라 생각되지만, 확실하지 않음)
여기에서는 stochastic(확률적) setting 에 deterministic attention을 적용시켜 Bayesian 관점에서 multi-head attention을 이해하려 한다.
extra trainalble parameter나 다른 규제를적용시키는 게 아니라 multi-head attention의 repulsiveness를 향상시킬 수 있는 새로운 알고리즘을 소개한다.
(head의 유사도를 Loss 로 해서 repulsive 구현)
Bayesian interpretation을 통해 multi-head의 이점을 소개.
2 Preliminaries
2.1 Multi-head Attention
2.2 Particle-optimization Sampling
particle density와 target p 사이의 KLdivergence를 작게하는 방향으로 Particle/sample 세트를 target distribution p로 보내는 것
여기에서, p는 사후확률로 p(θ|D) ∝ exp(−U(θ))이고, D는 관찰된 데이터셋이다. U는 potential enrergy를 나타낸다
여기에서 θ 는 model parameter로, 이 예제에서는 q의 가중치와 같은 attention parameter로 볼 수 있다.
particle-optimization sampling에서는 p(θ|D)예측을 위해 {θ (i)} (i=1~M) 가 업데이트된다. 이 논문에서는 update를 위해 Stein Variational Gradient Descent (SVGD) and the Stochastic ParticleOptimization Sampling (SPOS)를 이용한다.
SVGD
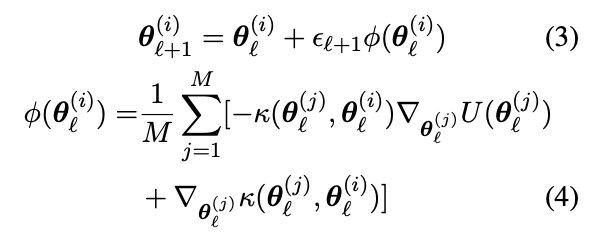
The two terms in φ play different roles: the first term drives the particles towards high density regions of p(θ|D);
second term : a repulsive force that prevents all the particles from collapsing together into local modes of p(θ|D).
particle 이 특정 분포를 취해야하기 때문에 particle이 target의 피크에 가고자 하는 것과 한 쪽에 쏠리는 것을 막는 요소가 존재.
SPOS
SVGD에서 particle 들이 충돌하려고 하는 문제 발생. -> SVGD에 random noise 를 추가

3 A Bayesian Inference Perspective of Multi-head Attention
particle-optimization sampling을 이용하여 multi-haed attention을 Bayesian 형식으로 표현.
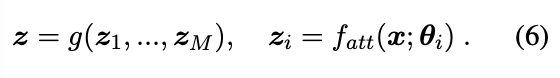
attention feature 을 위와 같이 표현 가능.
여기에서 세타에 stochastic gernerative process를 진행하면,

위와 같이 표현 가능하고, 여기에 베이지안 rule과, 연속함수에서의 법칙을 적용시키면 아래와 같이 나온다.



최종적으로 (7) 식과 같이 표현할 수 있는데, 이는 multi-head attention을 Bayeisan view 에서 나타낸 것임을 볼 수 잇다. 여기에서 θi 들이 p(θ|D) 분포를 공유하지 않으면, 독립적이라면 standard multi-attention 식과 유사함을 볼 수 잇다.
4 Repulsive Attention Optimization

(7)번 식을 이용하여 repulsive attention에 대한 idea를 얻을 수 있다. 이는 사후확률 p(θ|D)를 통해서 repulsive sample을 idea이다. -> sample 사이의 repulsiveness를 조장.(?) by particle-optimization sampling methods.
논문에서 제시한 알고리즘에서는 각 head의 p(z|x; θ) 를 하나의 particle 로 취급한다. particle-optimization rule에 따라 M heads {θi}M i=1 는 attention parameter p(θ|D)의 사후확률 분포를 예측하며 업데이트된다.
4.1 Learning Repulsive Multi-head Attention
기존의 attention에서는 각가의 head가 loss function과 gradient에 따라 독립적으로 업데이트된다. repulsive multi-head attention에서는 다른 파라미터의 업데이트는 하지 않은채, head의 Update만 진행하는 particle-optimization sampling update rule 을 따른다. -> 이 내용 이해를 위해서는 앞 부분 (3),(4),(5) 식의 이해가 필요할듯
4.2 In-depth Analysis
Why Multi-head Attention?
i)overfitting : 적은 데이터에서 오버피팅이 일어나고, 이때 더 적은 수의 head 가 필요하다.
ii) numerical error : attention-head parameter 들이 이산분포. -> sample 들이 target distribution을 따르지 않음. ?
particle-optimization sampling -> 더 많은 head -> error를 더 많이 축적할 수 있고, performance deterioration으로 이끌 수 잇음.
사후확률을 예측할 때, particle distribution과 true distribution 사이의 간극이 존재. = approximation error

How Many Heads are Enough?
apptoximation accuracy와 M(head 개수) 사이의 trade-off 존재.
-> M이 작으면 error가 작아짐.
-> M의 값에 대해서 정확히 정해진 바는 없지만, 무조건 많다고 좋은 performance는 아님.
SVGD term 이용, 두 head 사이의 regularization을 Loss term 에 추가해서 각각의 head를 떨어뜨리게함.

미묘한 성능차이 존재.
일반 attnetion 과 repulsive attention에서의 dropout을 적용시켰을 때 차이가 나는가?
head 가 몰려있는 중간에 repulsive를 적용시킨다면?
'논문읽기 > attention' 카테고리의 다른 글
| [논문읽기] DeepViT: Towards Deeper Vision Transformer (0) | 2022.02.17 |
|---|---|
| [논문읽기] 아직 발행X HOW DO VISION TRANSFORMERS WORK? (0) | 2022.01.24 |
| [논문읽기] Are Sixteen Heads Really Better than One? (0) | 2022.01.19 |
| [논문읽기] Accelerating Training of Transformer-BasedLanguage Models with Progressive Layer Dropping (0) | 2022.01.17 |
| [논문읽기] ON THE RELATIONSHIP BETWEEN SELF-ATTENTION AND CONVOLUTIONAL LAYERS (0) | 2022.01.16 |


