전반적으로 self- attention layer가 CNN을 대신할 수 있는가에 대한 논문.
1. 이론적으로 self-attention layer가 모든 convolutional layer를 나타낼 수 있다는 것을 증명
-> relative positioning encoding을 사용하는 multi-head self-attention layer가 모든 convolutional layer를 표현하는 방법으로 re-parameterize 가능하다는 것을 보이는 것이 목적.
2. 실험을 통해 attention의 첫 몇개의 layer가 query 주변의 pattern을 찾는 것과 비슷한 역할을 한다.?
-> 그러니까 attention의 layer가 pattern과 매칭하는 CNN이랑 비슷한 역할을 해줄 수 있다는 의미?
CNN의 방법이 주변과 pattern을 매칭해서 가장 비슷한 거 찾아내는 게 맞나
2.3 POSITIONAL ENCODING FOR IMAGES
이 부분이 중요한 것 같은데, 절대적인 key 의 좌표 대신, key 와 query 사이의 좌표차이를 사용하여 positional embedding을 진행한다.
// augmentation attention에서도 여기가 중요하게 나왔었는데, 상대적인 좌표를 써야 pattern을 생성할 수 있는건가?
3 SELF-ATTENTION AS A CONVOLUTIONAL LAYER
증명하고자 하는 main idea는 다음과 같습니다.
Theorem 1. A multi-head self-attention layer with Nh heads of dimension Dh, output dimen- sion Dout and a relative positional encoding of dimension Dp ≥ 3 can express any convolutional
layer of kernel size root(Nh) × root(Nh) and min(Dh, Dout) output channels.
위에 방법적인 설명이 있는데 사실 잘 못알아듣겠음...
PROOF OF MAIN THEOREM

위와 같이 softmax 값을 만드는 전단사 함수 f(h)가 존재한다면, 모든 X에 대해 MHSA(X) = Conv(X)를 만족시키는 Wval(h)가 존재한다는 것을 증명하는 lemma 입니다. / conv개수만큼 head 개수 사용, k를 주변부로 설정, (강제로 주변부 할당해서 conv랑의 연관성보임)
head 가 conv 면적만큼 존재, head 에서 하나씩 뽑아서 weight 곱하면 conv
Dn = Dout/ Nh -> 왜 이렇게 설정하는가?

lemma 2는 다음과 같이, lemma 1의 조건이었던, softmax의 정의를 만족시키는 전단사함수가 존재함을 보이는 방법입니다.
증명은 조금 건너뛰고 보면, lemma 1과 2로 인해서 모든 convolution layer를 (수식적으로) attention layer로 대체할 수 있음을 볼 수 있습니다.
4 EXPERIMENTS
이론적으로, attention layer가 convolution layer처럼 perform 할 수 있다는 것을 보였다. 이제, 실제로 attention layer가 convolutional layer처럼 행동하는지, quadratic and learned positional encoding 으로 살펴볼 것이다.
4.2 QUADRATIC ENCODING
처음으로, relative position encoding 이 식 (9)를 만족시킨다면, convolutional layer처럼 행동한다는 것을 증명한 것이다.

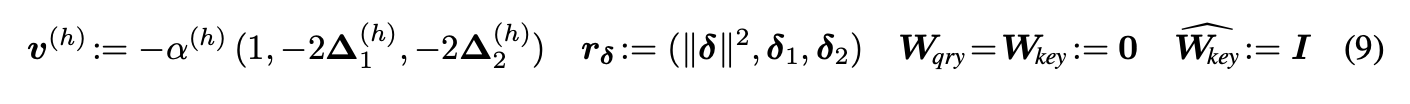
The center of attention of each head h is initialized to ∆(h) ∼ N (0, 2I2 ).
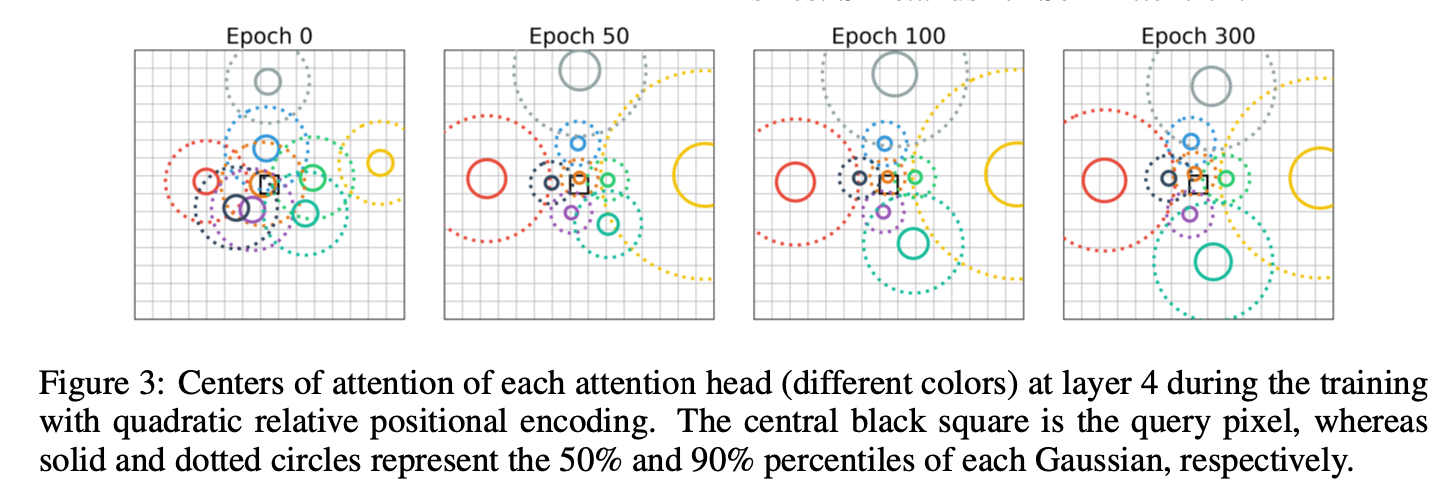
figure 3는 layer 4의 초기 head 의 위치를 나타내고 있는데요, optimizaiton 이 끝난후, 점점 query pixel 주위에 grid를 형성하는 모습을 볼 수 있습니다. -> 직관적으로 생각했던 query pixel 주변의 convolutional filter를 학습하는 모습을 볼 수 있습니다.
(갈수록 자신의 자리를 지킨다)
& 위에서 나타낸 원은 head의 위치가 아닌, 저 부분과의 attention을 수행했을 때 그 head 에서의 유사도가 가장 크게 나왔다. 라고 보는 게 맞을 것 같습니다.
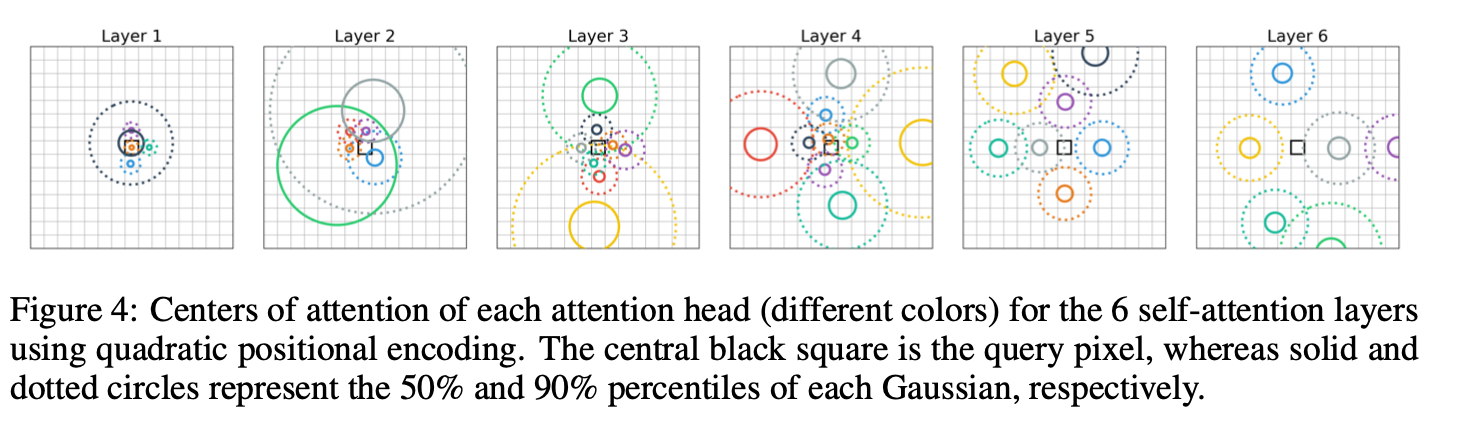
또한 figure 4에서 볼 수 있듯이, layer가 깊어질수록 long-dependencies를 확인함을 볼 수 있습니다. (과연 conv와의 연관성은?)
conv가 MHSA의 subset이다 /
conv로 multihead attention 을 만들수 있는가?(relative position에 conv값 넣으면 같음) -> conv처럼 구성한 MHSA는 같은 효과를 내는가?
앞단에서는 주로 local로 / 뒤에서는 conv를 hierical 하게 쌓은것처럼 먼 거리를 본다.
앞단에서 차원이 낮고, 주변을 살피는데 굳이 attention을 써야할까? & head 개수가 저렇게 많아야할까?
4.3 LEARNED RELATIVE POSITIONAL ENCODING
relative encoding을 학습하면 어떻게 되는가?
(Q+P)K. (P가 conv역할) -> 그런데 동시에 학습한 결과가 가장 안좋았음.
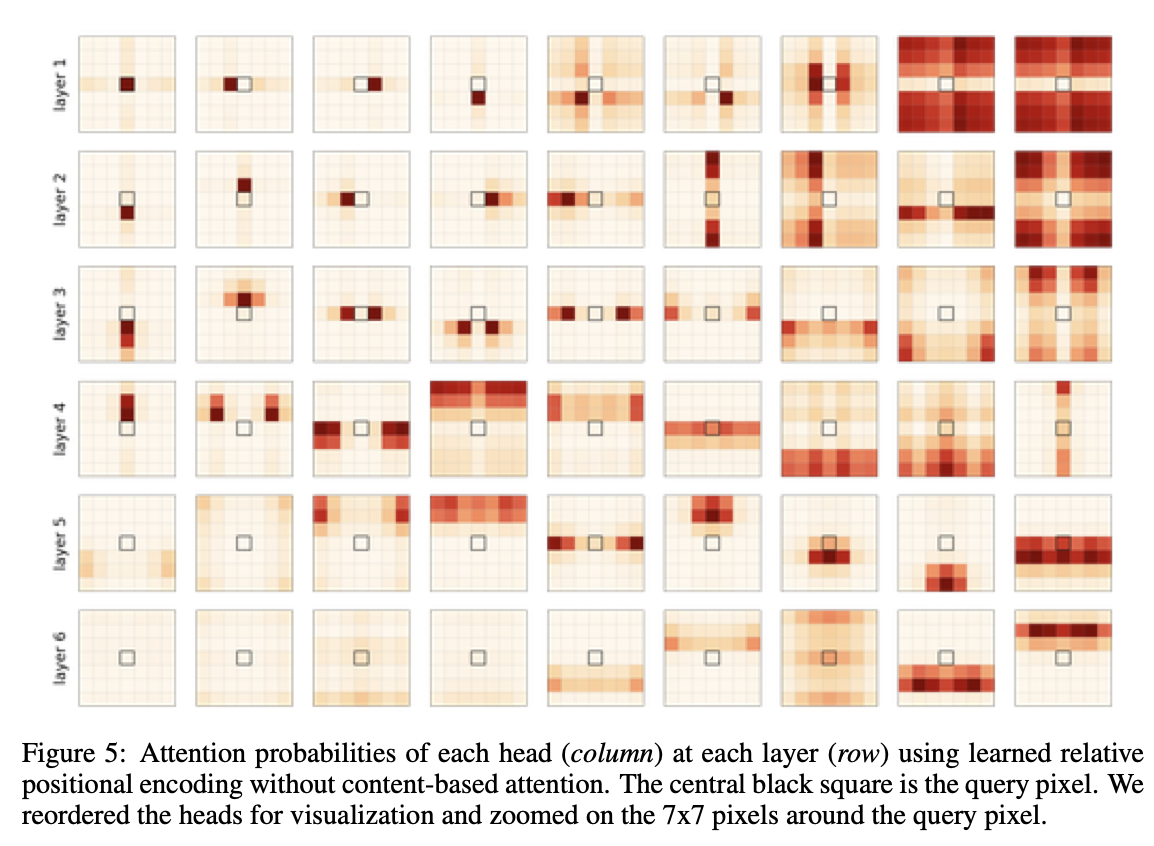
한 pixel을 중심으로(query)로 설정하고 봤을 때, conv처럼 동작하는 모습
왜 성능이 더 나빠질까?



