1. Introduction
CNN기법이 많이 쓰이고 있는데, global context를 파악하기에 어려움이 있다. Self-attention 은 hidden units의 weighted average value를 구하는 것인데, pooling 이나 convolutional operation과 다르게 weighted average value는 hidden units의 simularity를 계산하는 것으로 볼 수 있다. 이는 convolution 처럼 location의 영향을 받지 않으므로 parameter수의 인상 없이 Long-range interaction을 수행할 수 있다.
이 논문에서는 self-attention과 convolution을 모두 사용하여 multi-head의 결과와 기존 convolution의 결과를 concate하여 사용한다.

기존 attnetion과의 차이(BAM,CBAM 등)
reweight 하는게 아니라. 새로운 텐서 만듦. (? 두가지 관점으로 보는게 아니라, 합쳐서 봄)
3. Methods
Attention Aug- mentation method 소개.
following naming conven- tions: H, W and Fin refer to the height, width and number of input filters of an activation map. Nh, dv and dk respec- tively refer the number of heads, the depth of values and the depth of queries and keys in multihead-attention (MHA). We further assume that Nh divides dv and dk evenly and denote dhv and dhk the depth of values and queries/keys per attention head
3.1. Self-attention over images
Transformer architecture에 소개된 multi-head attention을 사용한다. 식은 아래와 같다.

queries Q = XWq, keys K = XWk and values V = XWv
이 output들에 아래식처럼 concate, projection이 시행된다.
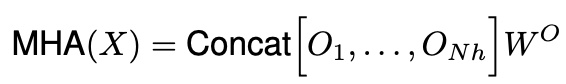
MHA(X)의 사이즈는 (H,W,dv)로 표현된다.
complexity of O((HW)2dk) and a memory cost of O((HW)2Nh)
3.1.1 Two-dimensional Positional Encodings
position 이 명확하지 않다면, self-attention은 permutation equvariant 하다. 이는 image에 있어서 효과가 없을 수 있다.

Relative positional encodings : translation equivariance, 즉 이미지 위치가 변경되어도 해당 객체 인식을 해야하기 때문에 상대적인 위치로 인코딩을 해준다
3.2. Attention Augmented Convolution

Conv(X) dim : H*W*dv
MHA(X) dim : H*W*(Fout-dv)
output : H*W*Fout
local 정보와 global 정보 mix
-> argmax를 실행할 때 두 개의 정보를 다 본다는 의미로 봐야하는건가?
conv와 attention의 병렬적 실행.
성능 :
병렬적 실행인데 왜 직렬적 실행(CoatNet) 보다 성능이 안좋게 나올까?
병렬적으로 쌓는것의 의미는?


